fjjackso
All American
14538 Posts
user info
edit post |
find the eigenvalues and (right/column) eigenvectors of the matrix
A= |2 -1 |
|3 -2 |
AND
Express the vector | 3 |
| 5 | as a linear combination of the eigenvectors of A.
not asking for someone to give me the answer, just trying to understand the process.  1/24/2007 1:33:20 PM 1/24/2007 1:33:20 PM
|
1985
All American
2174 Posts
user info
edit post |
The following statements are equivalent.
i) c is a characteristic value of A
ii)det(A-cI)=0.
were I is the identity matrix.
That should get you started.  1/24/2007 1:54:55 PM 1/24/2007 1:54:55 PM
|
virga
All American
2019 Posts
user info
edit post |
yeah, solve the polynomial generated by det(A-lambda*I)=0, and that will give you the eigen values. plug those back in to get the eigen vectors.  1/24/2007 2:01:53 PM 1/24/2007 2:01:53 PM
|
fjjackso
All American
14538 Posts
user info
edit post |
ok for the first part i got the eigen values to be (1,-1)... that checked out when I did the calculations on matlab....
but when I plug them back in, trying to get the eigenvectors, I got (1,-1/3) for -1 and (1,-1) for +1. matlab says the answer is (1,3) and (1,1) respectively. Can anyone show me where I am going wrong... also... still need help on the 2nd part of my first question.
Thanks  1/24/2007 8:50:52 PM 1/24/2007 8:50:52 PM
|
1985
All American
2174 Posts
user info
edit post |
you're almost there. The vectors that you found were just the top row of your row reduced matrix. What you need is a vector x such that when you multiply x by your row reduced matrix, you get zero. 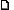 1/24/2007 10:47:28 PM 1/24/2007 10:47:28 PM
|
